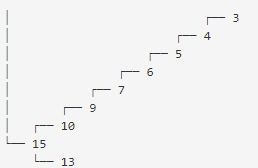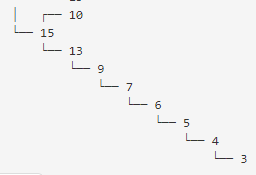Hi, I’m trying to solve the problem constructing a max-tree by array of distinct integers.
The idea is that we find max element from array (say with index m) and set it as root and left and right it’s descendents are max elements from (0, m-1) and (m+1, n) respectively. The algorithm complexity should be O(n).
I understand that array is an inorder traversal of the tree, but cannot realize what to do further.
I think I have managed to solve it. Comments welcome.
Firstly, let us consider the stack-less and recursion-less traversal of binary trees, where each node has a parent pointer.
This can be done by getting the leftmost node and successively getting the inorder successor. If a node has a right child, the inorder successor is the leftmost node in the right subtree. Otherwise, it is the first ancestor whose left child is an ancestor of given node.
For some nodes, getting the inorder successor may take O(height) time, but amortized over the whole tree, it takes O(n) time. Apologies for not proving this here; CLRS has a comprehensive proof. This fact will be used later on.
Secondly, observe the structure of the max-tree that will be created. It looks like a max heap. Hence, all root to node paths are strictly decreasing and similarly, all node to ancestor/root path is strictly increasing. This is an important point.
My algorithm scans the array from left to right, maintaining:
If the new node is a child, I recursively construct the right subtree keeping in mind to not exceed the array boundary and also, not to exceed the value of the current pointer (no child can exceed the value of an ancestor).
If the new node is a parent, we simply have to go to the root of the current tree being constructed (local to the function) and attach it as a left child of a new node.
Here (Github gist) is the solution and testing code in C++. The testing code works by comparing the trees created by my algo and the obvious O(n log n) solution.
Edit: Forget the inorder traversal complexity proof. I am never traversing the height of the tree in my solution and scanning each element only once. Time complexity is O(n).
Comments/Suggestions are welcome.
I think your method is correct (The problem number should be 10.10.2). I could not find any solution until reading your post.
The following is my implementation using stack, without recursion. I just tested it manually.
unique_ptr<BTNode<int>> ConstructMaxTree(const vector<int>& inputs) {
if (inputs.empty()) return nullptr;
stack<BTNode*> parents;
unique_ptr<BTNode<int>> root(new BTNode<int>{inputs[0]});
parents.emplace(root.get());
int cur = 1;
while (cur < inputs.size()) {
int cur_value = inputs[cur];
if (cur_value < parents.top()->data) {
parents.top()->right = unique_ptr<BTNode<int>>(new BTNode<int>{cur_value});
parents.emplace(parents.top()->right.get());
} else {
parents.pop();
while (!parents.empty() && parents.top()->data < cur_value)
parents.pop();
unique_ptr<BTNode<int>> new_node(new BTNode<int>{cur_value});
if (!parents.empty()) {
new_node->left = move(parents.top()->right);
parents.top()->right = move(new_node);
parents.emplace(parents.top()->right.get());
} else {
new_node->left = move(root);
root = move(new_node);
parents.emplace(root.get());
}
}
++cur;
}
return root;
}
/* Test 7 8 9 4 1 3 5 */Thank you for the explanation.
I think for some trees this: “we simply have to go to the root of the current tree being constructed” may take more than O(n) to construct. What if the parent of the element to be inserted is somewhere in the middle of the tree?
I mean what if you want to add 8 to the trees below (add something in between over and over again)?
First example:
Second example:
With the solution I posted, we are never going to insert somewhere in the middle of the tree. The way the construction will work is we will have a hanging forest of trees, mid-way in construction, that will all join in the end.
Why don’t you try pretty printing the binary tree at each step with ducalpha@'s test example and my code:
Also:
I was referring to an individual tree in this forest of trees that I described. The operation I described is an O(1) time operation. Have a look at this.
def get_root(arr, offset=0):
if offset >= len(arr):
return None
left_root = Node(arr[0])
while offset+1 < len(arr) and arr[offset+1] > arr[offset]:
larger_left_root = Node(arr[offset+1])
larger_left_root.left = left_root
left_root = larger_left_root
offset += 1
right_root = get_root(arr, offset+1)
lt_left = right_root
min_gt_left = None
while lt_left and lt_left.val > left_root.val:
min_gt_left = lt_left
lt_left = lt_left.left
left_root.right = lt_left
if min_gt_left:
min_gt_left.left = left_root
return right_root
else:
return left_root
def pprint(n, depth=0):
if not n:
return
pprint(n.right, depth+1)
print(" "*3*depth + str(n.val))
pprint(n.left, depth+1)
class Node:
def __init__(self, v):
self.val = v
from typing import Optional
self.right: Optional[Node] = None
self.left: Optional[Node] = None
pprint(get_root([2, 7, 9,1,3,6,4,8,5]))
Similar to sinha_kushagra, except right subtree is found later.
It finds increasing prefix of the current subarray which forms the left arm of current subtree. Then subtree for the remaining elements on the right is recursively created with root R. Then it scans the left arm of right subtree for the minimum element greater than left subtree’s root L. Call it E. Left subtree of E becomes right subtree of L and L becomes left subtree of E. If E is not found then R will be < L therefore R becomes right subtree of L.